Algoritma & Pengolahan Paralel
Gabungan preorder dan postorder traversal algoritma untuk analisis
of singular systems by Haar wavelets tunggal dari sistem oleh Haar wavelets
ABSTRAKSI
Pada penulisan ini, salah satu cara computational efisien disajikan untuk menyatakan analisa ruang dari sistem bentuk tunggal melalui riak Haar. Sistem bentuk tunggal adalah itu kemana dinamika diurus oleh satu kombinasi dengan secara aljabar dan persamaan diferensial. Diferensial sesuai penyamaan acuan secara aljabar dikonversi ke satu penyamaan disamaratakan acuan Sylvester dengan mempergunakan riak basis Haar. Pertama, satu ekspresi tegas untuk kebalikan dari acuan Haar disajikan. Kemudian ini penggunaan, kita mengajukan satu berkombinasi preorder dan algoritma postorder traversal untuk menyelesaikan penyamaan disamaratakan acuan Sylvester. Akhirnya efisiensi dari cara diusulkan didiskusikan oleh satu contoh kwantitatip.
Riak adalah berfungsi matematis yang memotong data ke dalam komponen frekuensi berbeda kemudian pembahasan masing-masing komponen dengan satu daya pisah mencocokan ke ini skalakan. Riak kini sedang teraplikasi pada beberapa area dari pengetahuan dan rancang-bangun [1] [4] Banyak perhatian telah difokuskan pada penggunaan dari riak mentransformasikan selidiki sistem dinamis. Ini sehubungan dengan kemampuan kuat dari riak mentransformasikan uraikan gugus berkala pada waktunya frekuensi basis daerah dan riak fungsi. Chen dan Hsiao [3] 4] perolehan satu acuan operasional Haar untuk integrasi dan terpecahkan lumped dan sistem parameter terdistribusi dengan membangun operasional acuan dari berbagai order. Karakteristik utama dari ilmu pengetahuan tentang teknik ini adalah yang ini mengonversi satu persamaan diferensial ke dalam satu sesuatu secara aljabar dengan hasil yang prosedur solusi sangat besar dikurangi dan sederhana. Pendekatan ini memberikan pengertian yang mendalam lagi ke dalam penggunaan dari riak Haar kiat.
Sistem bentuk tunggal (juga dikenal sebagai descriptor, atau sistem semistate) memunculkan lagi secara alami dibandingkan lakukan satu uraian variabel status pada analisa dari banyak berbagai dari sistem. Contoh terjadi pada jaringan elektrik, neural terhubung jaringan, sistem kendali, sistem kimia, ekonomi sistem, dan seterusnya( [5] 6] dan referensi pada hal itu). Sistem ini diurus oleh satu campuran diferensial dan penyamaan secara aljabar. Sifat alami kompleks dari lantaran sistem bentuk tunggal banyak kesulitan pada perlakuan analitis dan kwantitatip dari sistem demikian.
acuan operasional untuk integrasi dan terpecahkan lumped dan sistem parameter terdistribusi dengan membangun operasional acuan dari berbagai order. Karakteristik utama dari ilmu pengetahuan tentang teknik ini adalah yang ini mengonversi satu persamaan diferensial ke dalam satu sesuatu secara aljabar dengan hasil yang prosedur solusi sangat besar dikurangi dan sederhana. Pendekatan ini memberikan pengertian yang mendalam lagi ke dalam penggunaan dari riak Haar kiat
Sistem singular bentuk tunggal (juga dikenal sebagai descriptor, atau sistem semistate) memunculkan lagi secara alami dibandingkan lakukan satu uraian variabel status pada analisa dari banyak berbagai dari sistem. Contoh terjadi pada jaringan elektrik, neural terhubung jaringan, sistem kendali, sistem kimia, ekonomi sistem, dan seterusnya( [5] 6] dan referensi pada hal itu). Sistem ini diurus oleh satu campuran diferensial dan penyamaan secara aljabar. Sifat alami kompleks dari lantaran sistem bentuk tunggal banyak kesulitan pada perlakuan analitis dan kwantitatip dari sistem demikian.
Pada Penulisan ini, satu cara computational efisien disajikan untuk menyatakan analisa ruang dari sistem bentuk tunggal melalui riak Haar. Pertama, satu ekspresi tegas untuk kebalikan dari acuan Haar disajikan. Acuan kebalikan ini juga mempunyai satu struktur berulang. Dengan mempergunakan acuan ini, kita mengajukan satu berkombinasi preorder dan algoritma postorder traversal. Kemudian order penuh menyamaratakan acuan penyamaan Sylvester harus diselesaikan dalam kaitan dengan solusi dari acuan linear sederhana penyamaan. Akhirnya efisiensi dari cara diusulkan didiskusikan oleh satu contoh kwantitatip.
Produk Kronecker
Biar SATU [a ij ] ? dan B [b ij ] jadilah n x p dan r x q matrix, berturut-turut. Produk Kronecker dari matrix, ditandakan oleh

vec operator mentransformasikan satu acuan SATU dari ukuran n ´ p ke satu vektor ukuran n ´ p 1 oleh penumpukan kolom dari SATU . Beberapa hak milik dari produk Kronecker diberikan di bawah [8]
(A+B)ÄC=AÄC+BÄC
(AÄB)C=(ACÄB )
(AÄB)(CÄD)=(ACÄBD )
(AÄB) T =ATÄB T.
Riak Haar dan hak milik mereka
Riak mendasari sekeluarga dari fungsi membangun dari dilasi dan terjemahan dari fungsi tunggal panggil riak ibu yang menghasilkan orthogonal berlandaskan dari L2( R). Paling sederhana dan paling dasar sistem riak adalah riak Haar yang sekelompok dari gelombang cocok dengan kebesaran dari ± 1 pada interval tertentu dan antah-berantah nol [9] Fungsi kelupas φMemasuki ( t) dan asuh riak φ1 (t ) didefinisikan oleh, berturut-turut.

Kemudian, semua yang lain fungsi basis φ k (t ) diperoleh oleh dilasi dan terjemahan dari riak ibu sebagai berikut:
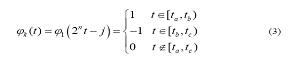
Dimana k = 2 n + j, bilangan bulat n = 1 adalah satu parameter dilasi, bilangan bulat memasuki = j< 2 n adalah satu parameter pergeseran, dan interval diberikan oleh  Sejak dukungan dari riak Haar adalah [0,1] apapun kuadrat integrable berfungsi y (t ) € l 2 [0,1) can be written as an infinite linear combination of Haar functions
Sejak dukungan dari riak Haar adalah [0,1] apapun kuadrat integrable berfungsi y (t ) € l 2 [0,1) can be written as an infinite linear combination of Haar functions 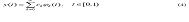
dimana koefisien Haar ditentukan olehdimana< . , . >tandakan produk dalam. Di aplikasi praktis, Rangkaian Haar dipotong ujung ke m kondisi, yang

Pm adalah m acuan operasional kuadrat dari integrasi yang mana memuaskan rumus berulang yang berikut [3]


Kita menyajikan berikut lemma yang mana biasanya menguraikan penyamaan disamaratakan acuan Sylvester.
Lemma 1 . Biar menjadi satu acuan Haar didefinisikan di (11). Kemudian acuan kebalikan ini punya bentuk berulang yang berikut: mH

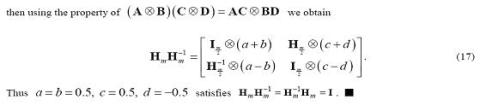
Sumber : klik disini
 Print this page
Print this page